2018 AMC 10A 试题/第1题
问题
的值是多少
\[ {\left( {\left( {\left( 2 + 1\right) }^{-1} + 1\right) }^{-1} + 1\right) }^{-1} + 1? \]
(A) \( \frac{5}{8} \) (B) \( \frac{11}{7} \) (C) \( \frac{8}{5} \) (D) \( \frac{18}{11} \) (E) \( \frac{15}{8} \)
解决方案
我们将从 \( 2 + 1 = 3 \) 开始,然后连续三次执行“取反加一”操作。经过三次迭代后得到: \( \frac{4}{3},\frac{7}{4} \) ,最终为 \( \left( \mathbf{B}\right) \frac{11}{7} \)
2018 AMC 10A 试题/第2题
问题
莉莲(Liliane)比杰奎琳(Jacqueline)多 \( {50}\% \) 的汽水,而爱丽丝(Alice)比杰奎琳多 \( {25}\% \) 的汽水。莉莲和爱丽丝拥有的汽水数量之间是什么关系?
(A) 莉莲的汽水比艾丽斯多 \( {20}\% \) 。
(B) 莉莲的汽水比爱丽丝多 \( {25}\% \) 。
(C) 莉莲的汽水比爱丽丝多 \( {45}\% \) 。
(D) 莉莲的汽水比艾丽斯多 \( {75}\% \) 。
(E) 莉莲的汽水比艾丽斯多 \( {100}\% \) 。
解决方案
假设Jacqueline有1加仑汽水,那么Alice有1.25加仑,Liliane有1.5加仑。通过除法计算,我们得出 \( \frac{1.5}{1.25} = {1.2} \) ,这意味着Liliane比Jacqueline多 \( {20}\% \) 汽水。因此,答案是(A) \( {20}\% \)
解法2
如果Jagqueline有 \( x \) 加仑汽水,Alice有 \( {1.25x} \) 加仑,Liliane有 \( {1.5x} \) 加仑。因此答案是 \( \frac{1.5}{1.25} = {1.2} \rightarrow \) Liliane多了 \( {20}\% \) 加仑汽水。我们的答案是 \( \left( \mathbf{A}\right) {20}\% \)
2018 AMC 10A试题/第3题
题目
一单位血液在 \( {10}! = {10} \cdot 9 \cdot 8\cdots 1 \) 秒后过期。Yasin在1月1日中午捐献了一单位血液。他的血液在哪一天过期?
(A) 1月2日 (B) 1月12日 (C) 1月22日 (D) 2月11日 (E) 2月12日
解法1
血液在过期前有 \( {10}! \) 秒,而一天有 \( {60} \cdot {60} \cdot {24} \) 秒。相除 \( \frac{10}{{60} \cdot {60} \cdot {24}} \) 得到42天。1月1日后42天是
解法2
题目说有 \( {10}! = {10} \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \) 秒。将 \( {10}! \) 秒除以60换算成分钟: \( 9 \cdot 8 \cdot 7 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \) 分钟。再将分钟除以60换算成小时: \( 9 \cdot 8 \cdot 7 \cdot 2 \) 小时。再将小时除以24换算成天: \( 3 \cdot 7 \cdot 2 = {42} \) 天。
现在需要计算1月1日后42天。由于从1月1日开始,这一天本身不能算。到1月31日(月底)时,我们只数了30天。 \( {42} - {30} = {12} \) 。再数12天,结果
(E) 2月12日
2018 AMC 10A试题/第4题
题目
一名学生要在6节课的一天中安排3门数学课——代数、几何和数论——有多少种排法,要求任意两门数学课不能连堂?(其余3节课上什么课无需考虑。)
(A) 3 (B) 6 (C) 12 (D) 18 (E) 24
解法1
我们必须把课程安排到课时中,使得任意两门课既不在同一课时,也不相邻。
不考虑可区分性,我们可以列出在不允许相邻的情况下,从六个课时中选出三个课时给课程的所有方式:
课时1、3、5
课时1、3、6
课时1、4、6
课时2、4、6
共有4种方式将3门不可区分的课程放入6个课时,且任意两门课不相邻。对每一种方式,课程内部又有 \( 3! = 6 \) 种排列。
因此,共有 \( 4 \cdot 6 = \) (E) 24种选择课程的方式。
-Versailles15625
解法2
意识到:在6课时的日程中,无论顺序如何,安排3门数学课且任意两门不相邻的方式数,与在4课时的序列中,无论顺序如何,安排3门数学课(无论是否相邻)的方式数相同。
为了看清这种一一对应关系,请注意:对于每一种在4课时中安排3门数学课的方式(如上所述),都可以在每对相邻出现的数学课之间(共2处)插入一门非数学课,从而确保在最终的6课时日程中不会出现两门数学课相邻。例如, \( M \) 表示数学课, \( O \) 表示非数学课: \( \overset{\widetilde{}}{\text{MO}}\overset{\widetilde{}}{\text{MO}}\overset{\widetilde{}}{\text{M}} \rightarrow \overset{\widetilde{}}{\text{MO}}\overset{\widetilde{}}{\text{O}}\overset{\widetilde{}}{\text{M}} \)
对于每一个由 \( M \) 和 \( O \) 组成的6课时序列,我们有 \( 3! \) 种对3门不同数学课的排列方式。
所以,我们的答案是 \( \left( \begin{array}{l} 4 \\ 3 \end{array}\right) \left( {3!}\right) = \left\lbrack {\left( \mathbf{E}\right) {24}}\right\rbrack \)
- Gregwwl
解法3
通过计算我们不想要的情况,是另一种巧妙的解题方法。使用容斥原理(PIE)计算两种情形:1. 两节课连续,2. 三节课连续。
情形1:把两个连续时段视为一个“块”,共有5个可放位置(1,2; 2,3; 3,4; 4,5; 5,6)。然后只需在该块内安排两节课, \( 3 \cdot 2 \) 。最后还剩4个时段可放最后一节数学课。因此,在不考虑第三节的情况下,共有 \( 5 \cdot 3 \cdot 2 \cdot 4 \) 种方式放置两节连续的数学课。
情形2:现在把三个连续时段视为一个“块”,共有4个可放位置 \( (1,2,3;2,3,4;3,4,5 \) ;4,5,6)。我们需要在该块内安排数学课, \( 3 \cdot 2 \cdot 1 \) 。因此,共有 \( 4 \cdot 3 \cdot 2 \cdot 1 \) 种方式放置三节全部连续的数学课。
根据容斥原理,我们用情形1减去情形2以避免重复计数: \( {120} - {24} \) 。然后从无任何限制的总放置方式中减去该结果: \( \left( {6 \cdot 5 \cdot 4}\right) - {96} = \) (E) 24
2018 AMC 10A 试题/第5题
Alice、Bob 和 Charlie 在徒步旅行,想知道离最近的城镇有多远。Alice 说:“我们至少离6英里。”Bob 回答:“我们最多离5英里。”Charlie 接着说:“其实最近的城镇最多离4英里。”结果三人的话都不对。设 \( d \) 为到最近城镇的距离(英里)。下列哪个区间是 \( d \) 所有可能值的集合?
(A)(0,4) (B)(4,5) (C)(4,6) (D)(5,6) (E) \( \left( {5,\infty }\right) \)
解法
由Alice和Bob可知 \( 5 < d < 6. \) ;由Charlie可知 \( 4 < d. \) 。将这两个区间取并集得到 \( \left( {D,6}\right) ,6 \) ,因为最近的城镇距离在5到6英里之间。
2018 AMC 10A 试题/第6题
题目
Sangho 向一个网站上传了一段视频,观众可以点赞或点踩。每段视频初始得分为0,每获1个点赞加1分,每获1个点踩减1分。某时刻 Sangho 看到自己的视频得分为90,且该视频获得的点赞票占已投票总数的65%。此时 Sangho 的视频共被投了多少票?
(A) 200 (B) 300 (C) 400 (D) 500 (E) 600
解法
如果 \( {65}\% \) 的票是点赞,那么的票是点踩。,所以90分相当于总票数的。简单心算可知答案为
2018 AMC 10A 试题/第7题
对于多少个(不一定为正)整数值的 \( n \) , \( {4000} \cdot {\left( \frac{2}{5}\right) }^{n} \) 的值为整数?
(A) 3 (B) 4 (C) 6 (D) 8 (E) 9
解答
4000的质因数分解为 \( {2}^{5} \cdot {5}^{3} \) 。因此, \( n \) 的最大值为3,最小值为-5。于是我们需要求从-5到3的范围,即 \( 3 - \left( {-5}\right) + 1 = 8 + 1 = \) (E) 9
2018 AMC 10A 试题/第8题
Joe有23枚硬币,包括5分硬币、10分硬币和25分硬币。他的10分硬币比5分硬币多3枚,且这些硬币的总价值为320分。Joe的25分硬币比5分硬币多多少枚?
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
解答1
设 \( x \) 为Joe拥有的5分硬币数量。因此,他必须有 \( \left( {x + 3}\right) \) 枚10分硬币和 \( \left( {{23} - \left( {x + 3}\right) - x}\right) \) 枚25分硬币。由于这些硬币的总价值为320分,我们可以写出
\( {5x} + {10}\left( {x + 3}\right) + {25}\left( {{23} - \left( {x + 3}\right) - x}\right) = {320} \Rightarrow {5x} + {10x} + {30} + {500} - {50x} = {320} \Rightarrow {35x} = {210} \Rightarrow \) Joe有6枚5分硬币、9枚10分硬币和8枚25分硬币。因此,答案为 \( 8 - 6 = \) (C) 2 ~Nivek
解答2
设 \( n \) 为Joe拥有的5分硬币数量,d为10分硬币数量, \( q \) 为25分硬币数量。我们要求的是 \( q - n \) 。
我们知道这些硬币的总价值为320分。于是有 \( 5\mathrm{n} + {10}\mathrm{\;d} + {25}\mathrm{q} = {320} \) 。记为(1)。
我们知道共有23枚硬币。于是有 \( n + d + q = {23} \) 。记为(2)。
我们知道10分硬币比5分硬币多3枚,这也意味着5分硬币比10分硬币少3枚。于是有 \( d - 3 = n \) 。
将d-3代入另外两个方程, \( \mathrm{n},\left( 1\right) \) 变为 \( 2\mathrm{\;d} + \mathrm{q} - 3 = {23} \) ,(2)变为 \( {15}\mathrm{\;d} + {25}\mathrm{q} - {15} = {320} \) 。(1)于是变为 \( 2\mathrm{\;d} + \mathrm{q} = {26} \) ,(2)于是变为 \( {15}\mathrm{\;d} + {25}\mathrm{q} = {335} \) 。
将(1)乘以25,我们得到 \( {50}\mathrm{\;d} + {25}\mathrm{q} = {650} \) (或 \( {25}^{ \land }2 + {25} \) )。用(1)减去(2)得到 \( {35}\mathrm{\;d} = {315} \) ,这意味着d=9。
将 \( d \) 代入 \( d - 3 = n, n = 6 \) 。
将 \( d \) 和 \( q \) 代入本题最初给出的(2), \( q = 8 \) 。
因此,答案是 \( 8 - 6 = \) (C) 2
解法3
于是你把5分硬币的数量设为x,10分硬币的数量设为x+3,25分硬币的数量设为y。
你列出两个方程:
\[ {5x} + {10}\left( {x + 3}\right) + {25y} = {320} \Rightarrow {15x} + {25y} + {30} = {320} \Rightarrow {15x} + {25y} = {290} \]
\[ x + x + 3 + y = {23} \Rightarrow {2x} + 3 + y = {23} \Rightarrow {2x} + y = {20} \]
接着,你把第二个方程乘以25得到
\[ {50x} + {25y} = {500} \]
用乘以25后的第二个方程减去第一个方程得到
\[ {35x} = {210} \Rightarrow x = 6 \]
你可以把这个值代入其中一个方程得到
\[ y = 8 \]
所以,答案是 \( 8 - 6 = \) (C) 2
2018 AMC 10A 试题/第9题
题目
下图中的所有三角形都与等腰三角形 \( {ABC} \) 相似,其中 \( {AB} = {AC} \) 。7个最小三角形每个面积为1, \( \bigtriangleup {ABC} \) 的面积为40。梯形 \( {DBCE} \) 的面积是多少?
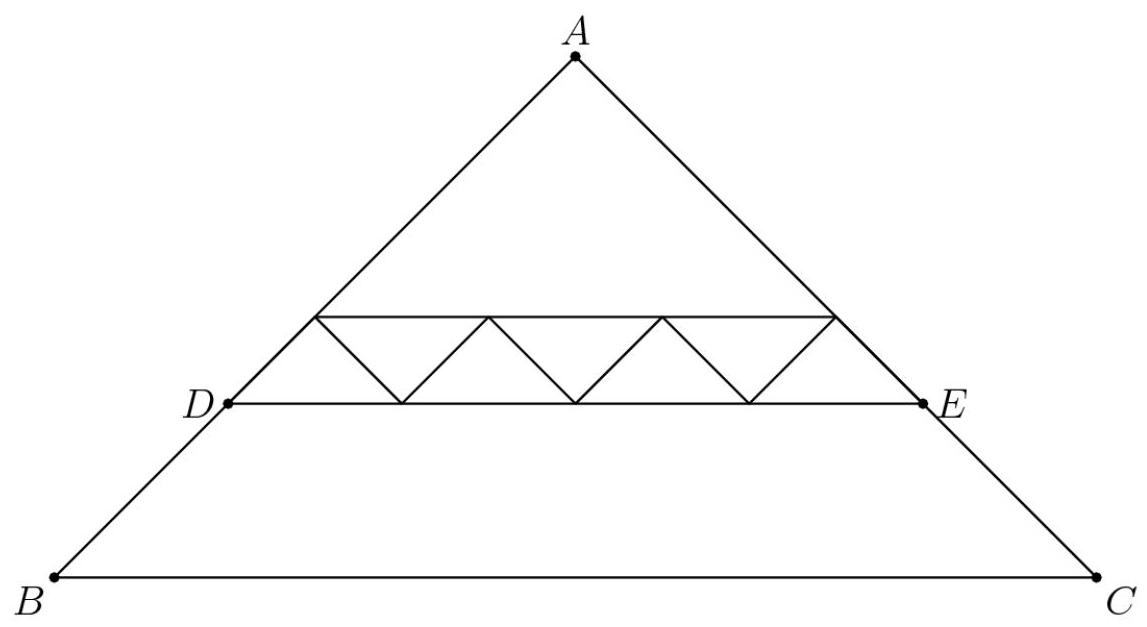
(C) 20 (D) 22 (E) 24 解法1 设 \( x \) 为 \( {ADE} \) 的面积。注意 \( x \) 由7个小等腰三角形和一个与 \( {ADE} \) 相似且边长比为 \( 3 : 4 \) (因此面积比为 \( 9 : {16} \) )的三角形组成。于是我们有
\[ x = 7 + \frac{9}{16}x \]
由此得到 \( x = {16} \) ,因此
解法2
设小三角形的底边长度为 \( x \) 。于是存在一个三角形 \( {ADE} \) ,它包含7个小三角形,并与它们共享顶角,其底边长度为 \( {4x} \) 。由于面积与边长的平方成正比,设底边 \( {BC} \) 为 \( \sqrt{40}x \) ,则三角形 \( {ADE} \) 的面积为16。因此面积为 \( {40} - {16} = {24} \) 。
解法3
注意到 \( \lceil {DBCE}\rceil = \lceil {ABC}\rceil - \lceil {ADE}\rceil \) 。设面积为1的小三角形的底边为 \( x \) ,则底边长度
\[ \text{of}\bigtriangleup {ADE} = {4x}\text{. Notice,}{\left( \frac{DE}{BC}\right) }^{2} = \frac{1}{40} \Rightarrow \frac{x}{BC} = \frac{1}{\sqrt{40}}\text{, then} \]
\[ {4x} = \frac{4BC}{\sqrt{40}} \Rightarrow \left\lbrack {ADE}\right\rbrack = {\left( \frac{4}{\sqrt{40}}\right) }^{2} \cdot \left\lbrack {ABC}\right\rbrack = \frac{2}{5}\left\lbrack {ABC}\right\rbrack \text{Thus,} \]
\[ \left\lbrack {DBCE}\right\rbrack = \left\lbrack {ABC}\right\rbrack - \left\lbrack {ADE}\right\rbrack = \left\lbrack {ABC}\right\rbrack \left( {1 - \frac{2}{5}}\right) = \frac{3}{5} \cdot {40} = {24} \]
ktong 提供解法
解法4
\( {ADE} \) 的面积是小三角形面积的16倍,因为二者相似且边长比为 \( 4 : 1 \) 。因此梯形面积为 \( {40} - {16} = {24} \) 。
解法5
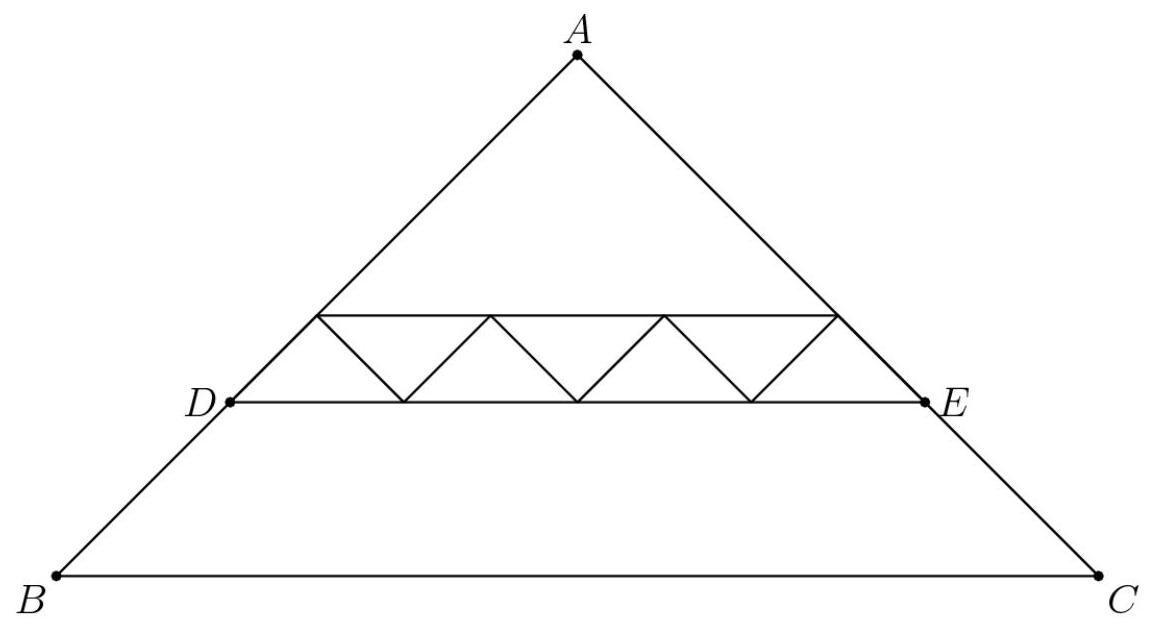
可以看到,我们可以把5个与图中7个小三角形全等的三角形“堆叠”成一行,放在这7个三角形之上,其总面积为5。同理,再堆一行3个,最顶端再放1个,如下所示。已知累积面积为 \( 7 + 5 + 3 + 1 = {16} \) ,于是梯形 \( {BCED} \) 的面积只需取 \( {40} - {16} = {24} \) ,如下。∎ --anna0kear
解法6
小三角形的总面积为7,且每个小三角形面积为1,可推知上方大三角形面积为9(因为三角形边长比例为 \( \frac{1}{3} \) ,面积比例则为边长比例的平方,即 \( \frac{1}{9} \) )。于是顶部三角形与其正下方梯形合并的面积为 \( 7 + 9 = {16} \) 。因此梯形 \( {BCED} \) 的面积即为三角形 \( {ABC} - {16} = {24} \) 的面积。--lepetitmoulin
2018 AMC 10A 试题/第10题
题目
设实数 \( x \) 满足
\[ \sqrt{{49} - {x}^{2}} - \sqrt{{25} - {x}^{2}} = 3 \]
求 \( \sqrt{{49} - {x}^{2}} + \sqrt{{25} - {x}^{2}} \) 的值?
\( \textbf{(A)}8\;\textbf{(B)}\sqrt{33} + 8\;\textbf{(C)}9\;\textbf{(D)}2\sqrt{10} + 4\;\textbf{(E)}{12} \)
解答
解法1
为了消去平方根,我们乘以共轭式,其值即为所求。含 \( {x}^{2} \) 的项恰好抵消。
\( \left( {\sqrt{{49} - {x}^{2}} + \sqrt{{25} - {x}^{2}}}\right) \left( {\sqrt{{49} - {x}^{2}} - \sqrt{{25} - {x}^{2}}}\right) = {49} - {x}^{2} - {25} + {x}^{2} = {24} \)
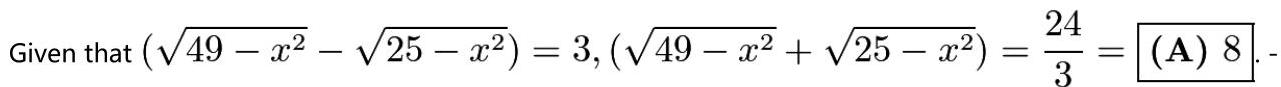
cookiemonster2004
解法2
设 \( u = \sqrt{{49} - {x}^{2}} \) ,并设 \( v = \sqrt{{25} - {x}^{2}} \) 。则 \( v = \sqrt{{u}^{2} - {24}} \) 。代入后得到
\( u - \sqrt{{u}^{2} - {24}} = 3 \) 。整理得 \( u - 3 = \sqrt{{u}^{2} - {24}} \) 。两边平方并求解,得到
\( u = \frac{11}{2} \) 和 \( v = \frac{11}{2} - 3 = \frac{5}{2} \) 。相加后可知答案为(A) 8。
解法3
将方程移项。 \( \sqrt{{49} - {x}^{2}} - \sqrt{{25} - {x}^{2}} = 3 \) 可改写为
\( \sqrt{{49} - {x}^{2}} = \sqrt{{25} - {x}^{2}} + 3 \) .
两边平方,得到 \( {49} - {x}^{2} = \left( {{25} - {x}^{2}}\right) + \left( {3}^{2}\right) + 2 \cdot 3 \cdot \sqrt{{25} - {x}^{2}} \) 。
化简得 \( {15} = 6\sqrt{{25} - {x}^{2}} \) 。两边除以6得 \( \frac{5}{2} = \sqrt{{25} - {x}^{2}} \) 。
接着再次两边平方,得到方程 \( \frac{25}{4} = {25} - {x}^{2} \) 。化简后得
\[ {x}^{2} = \frac{75}{4}. \]
代入方程 \( \sqrt{{49} - {x}^{2}} + \sqrt{{25} - {x}^{2}} \) ,得到 \( \sqrt{{49} - \frac{75}{4}} + \sqrt{{25} - \frac{75}{4}} \) 。立即化简为 \( \sqrt{\frac{121}{4}} + \sqrt{\frac{25}{4}} \) 。根号内的两个数化简为 \( \frac{11}{2} \) 和 \( \frac{5}{2} \) ,因此相加得 \( \frac{11}{2} + \frac{5}{2} = \) (A) 8
解法4(几何解释)
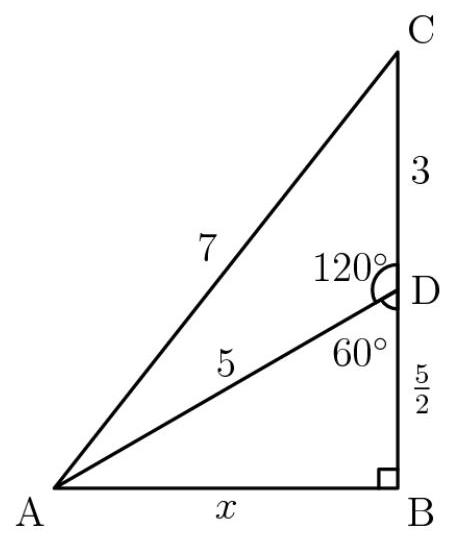
作直角三角形 \( {ABC} \) ,斜边 \( {AC} \) 长7,直角边 \( {AB} \) 长 \( x \) 。在 \( {BC} \) 上取 \( D \) ,使得 \( {AD} = 5 \) 。注意 \( {BC} = \sqrt{{49} - {x}^{2}} \) 且 \( {BD} = \sqrt{{25} - {x}^{2}} \) 。于是由给定方程得 \( {BC} - {BD} = {DC} = 3 \) 。对三角形 \( {ADC} \) 应用余弦定理,可见 \( \angle {ADC} = {120}^{ \circ } \) ,因此
\( \angle {ADB} = {60}^{ \circ } \) . 由于 \( {ADB} \) 是一个 \( {30} - {60} - {90} \) 三角形, \( \sqrt{{25} - {x}^{2}} = {BD} = \frac{5}{2} \) 且
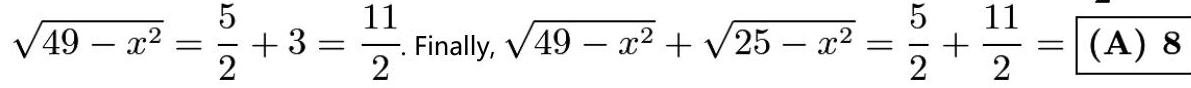
2018 AMC 10A 试题/第11题
当投掷7颗公平的6面骰子时,朝上面数字之和为10的概率可表示为
\[ \frac{n}{{6}^{7}} \]
其中 \( n \) 为正整数。 \( n \) 是多少?
(A) 42 (B) 49 (C) 56 (D) 63 (E) 84
解答
解法1
骰子朝上面最小为1,因此7颗骰子朝上面数字之和的最小值为7。
要使和恰好为10,需将1到3颗骰子的朝上面数字共增加3。
共有3种方式: \( 3,2 + 1 \) ,以及 \( 1 + 1 + 1 \)
情况1有7种,情况2有 \( 7 * 6 = {42} \) 种,情况3有 \( \frac{7 * 6 * 5}{3!} = {35} \) 种。
因此答案为 \( 7 + {42} + {35} = \) (E)84
由PancakeMonster2004提供 解法2
用7颗骰子掷出总和10可用“星与条”表示:10颗星和6条竖线。每颗星代表骰子面上的一个点,竖线分隔不同骰子。但需注意每颗骰子至少有一个点,因此已预先有7颗星。剩下3颗星和6条竖线,可重排为 \( \left( \begin{array}{l} 9 \\ 3 \end{array}\right) = \left( {\mathbf{E}8}\right) {84} \) 种方式。(RegularHexagon)
解法3
累加可能性。共有3种方式使和为10,如下所列。
\[ 4,1,1,1,1,1,1 : 7 \]
\[ 3,2,1,1,1,1,1 : {42} \]
\[ 2,2,2,1,1,1,1 : {35}\text{.} \]
把所有可能性加起来: \( {35} + {42} + 7 = \) (E) 84
因此,我们完全重复了解法1,只是解释更少。
解法4(杀鸡用牛刀)
我们可以使用生成函数,其中 \( \left( {x + {x}^{2} + \ldots + {x}^{6}}\right) \) 是每一颗骰子的函数。我们需要求 \( {\left( x + {x}^{2} + \ldots + {x}^{6}\right) }^{7} \) 中 \( {x}^{10} \) 的系数,也就是 \( {\left( \frac{1 - {x}^{7}}{1 - x}\right) }^{7} \) 中 \( {x}^{3} \) 的系数。计算结果为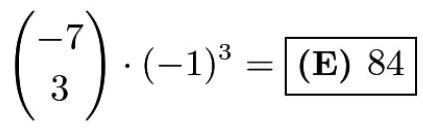
2018 AMC 10A 试题/第12题
有多少个有序实数对(x, y)满足以下方程组?
\[ x + {3y} = 3 \]
\[ \left| \right| x\left| -\right| y\left| \right| = 1 \]
\( \textbf{(A)}\;1\;\textbf{(B)}\;2\;\textbf{(C)}\;3\;\textbf{(D)}\;4\;\textbf{(E)}\;8 \)
解法
解法1
我们可以通过画图来解这个方程组。第二个方程看起来很难画,但可以先只在第一象限画图(此时可以忽略内部的绝对值符号,因此很容易),然后把图像反射到其他象限即可。
图像大致如下:
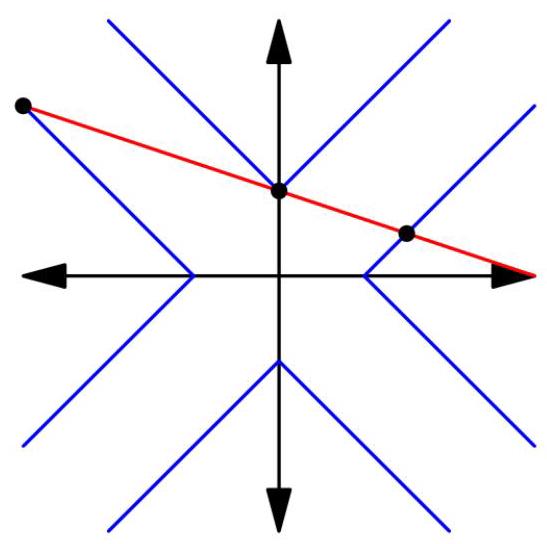
现在可以清楚地看到共有 \( \left( {\mathbf{C}\mathbf{)}3}\right) \) 个交点。(pinetree1) BOI
解法2
\( x + {3y} = 3 \) 可以改写为 \( x = 3 - {3y} \) 。将 \( 3 - {3y} \) 代入第二个方程中的 \( x \) ,得到 \( \left| \right| 3 - {3y}\left| {-y}\right| = 1 \) 。根据 \( y \) 的取值范围分情况讨论,即可得到解的总数。
情况1: \( y > 1 \) : \( 3 - {3y} \) 为负,因此 \( \left| {3 - {3y}}\right| = {3y} - 3.\left| {{3y} - 3 - y}\right| = \left| {{2y} - 3}\right| = 1 \)
子情况 \( 1 : y > \frac{3}{2} \)
1 \( {2y} - 3 \) 为正,因此 \( {2y} - 3 = 1 \) 且 \( y = 2 \) 且 \( x = 3 - 3\left( 2\right) = - 3 \) 子情况 \( 2 : 1 < y < \frac{3}{2} \) \( {2y} - 3 \) 为负,因此 \( \left| {{2y} - 3}\right| = 3 - {2y} = 1 \) 。 \( {2y} = 2 \) ,故无解( \( y \) 不能等于1) 情况2: \( y = 1 \) :显然 \( x = 0 \) 。 情况3: \( y < 1 : 3 - {3y} \) 为正,因此 \( \left| {3 - {3y} - y}\right| = \left| {3 - {4y}}\right| = 1 \) 子情况 \( 1 : y > \frac{4}{3} \) \( 3 - {4y} \) 为负,因此 \( {4y} - 3 = 1 \rightarrow {4y} = 4 \) 。同样无解( \( y \) 不能等于1)
子情况 \( 2 : y < \frac{4}{3} \) \( 3 - {4y} \) 将为正,因此 \( 3 - {4y} = 1 \rightarrow {4y} = 2 \) 。 \( y = \frac{1}{2} \) 且 \( x = \frac{3}{2} \) 。于是,解为: \( \left( {-3,2}\right) ,\left( {0,1}\right) ,\left( {\frac{3}{2},\frac{1}{2}}\right) \) ,答案是(C) 3。LATEX由pretzel编辑,Bryanli做了极小的LATEX调整,ssb02做了非常非常小的LATEX调整
解法3
注意 \( \left| \right| x\left| -\right| y\left| \right| \) 可以取四个值之一: \( x + y \) 、 \( x - y \) 、 \( - x + y \) 、 \( - x - y \) 。通过消元法(将两方程相加或相减)求解,我们得到三个解:(0,1)、(-3,2)、(1.5,0.5),因此答案是 \( \Gamma {\mathbf{\left( C\right) }\text{ 3 }} \) 。其中一条方程与(0,1)重合,所以只有3个解。
~trumpeter, ccx09 ~小修改,XxHalo711
解法4
与解法2相同,我们推导出方程 \( \left| \right| 3 - {3y}\left| -\right| y\left| \right| = 1 \) 。若去掉绝对值,方程可化为四种可能值: \( 3 - {2y} \) 、 \( 3 - {4y} \) 、 \( {2y} - 3 \) 和 \( {4y} - 3 \) ,每个都等于1或-1。记住若 \( P - Q = a \) ,则 \( Q - P = - a \) 。由于已考虑1和-1,可去掉每对共轭中的一个,即 \( 3 - {2y} \) 和 \( {2y} - 3 \) , \( 3 - {4y} \) 和 \( {4y} - 3 \) 。求 \( y \) 在 \( 3 - {2y} = 1 \) 、 \( 3 - {2y} = - 1 \) 、 \( 3 - {4y} = 1 \) 和 \( \underline{3 - {4y} = - 1} \) 时的值。我们发现 \( 3 - {2y} = 1 \) 和 \( 3 - {4y} = - 1 \) 给出相同的 \( y \) 值,因此答案是 \( \mathbf{\left( C\right) }3 \)
2018 AMC 10A 试题/第13题
题目
如图所示,一个边长为3、4、5英寸的纸三角形被折叠,使点 \( A \) 落在点 \( B \) 上。折痕的长度是多少英寸?
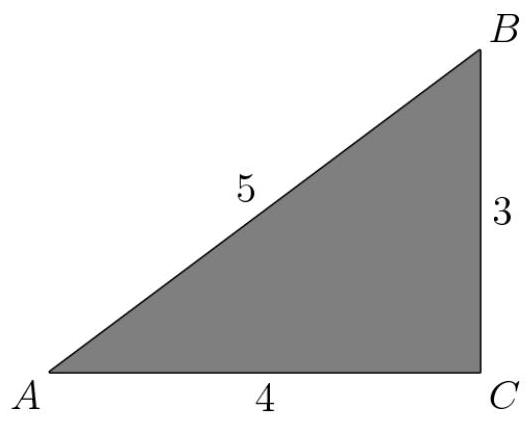
(A) \( 1 + \frac{1}{2}\sqrt{2} \) (B) \( \sqrt{3} \) (C) \( \frac{7}{4} \) (D) \( \frac{15}{8} \) (E) 2
解法1
首先,我们需认识到折痕就是边 \( {AB} \) (直角三角形 \( \bigtriangleup {ABC} \) 的斜边)的垂直平分线。设 \( {AB} \) 的中点为 \( D \) 。画出该线,并设其与 \( {AC} \) 的交点为 \( E \) 。此时, \( \bigtriangleup {ACB} \) 与 \( \bigtriangleup {ADE} \) 通过 \( {AA} \) 相似。列出比例,我们得到
\[ \frac{BC}{AC} = \frac{DE}{AD} \Rightarrow \frac{3}{4} = \frac{DE}{\frac{5}{2}} \Rightarrow {DE} = \frac{15}{8}. \]
因此,我们的答案是 \( DD\frac{15}{8} \)
注
一般而言,每当要求折一条折痕时,应把这条折痕视为一条反射轴,整个图形将沿此轴反射。因此,这条折痕必须是 \( {AB} \) 的垂直平分线,因为 \( A \) 必须被反射到 \( B \) 。(by pulusona)
解法2
用你带来的直尺和方格纸,迅速画出任意比例的3-4-5三角形(别相信小册子里的图)。非常小心地把两个锐角顶点对折在一起,并压出折痕。用直尺量这条折痕。如果你足够仔细,会发现它的长度略大于 \( \frac{7}{4} \) 单位,又略小于2单位。
唯一在范围内的选项是
这基本算投机取巧,但规则上确实允许。
2018 AMC 10A 试题/第14题
小于或等于该值的最大整数是多少?
\[ \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}}? \]
(A) 80 (B) 81 (C) 96 (D) 97 (E) 625
解法 解法1
设该值为 \( x \) 。我们可以写成
\[ \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}} = x. \]
两边同乘以 \( {3}^{96} + {2}^{96} \) ,得到
\[ {3}^{100} + {2}^{100} = x\left( {{3}^{96} + {2}^{96}}\right) . \]
现在看看选项。我们注意到81,即选项 \( B \) ,可写成 \( {3}^{4} \) 。将其代入上方方程,得到
\[ {3}^{100} + {2}^{100}\overset{?}{ = }{3}^{4}\left( {{3}^{96} + {2}^{96}}\right) \Rightarrow {3}^{100} + {2}^{100}\overset{?}{ = }{3}^{100} + {3}^{4} \cdot {2}^{96}. \]
右侧大于左侧,因为
\[ {2}^{100} \leq {2}^{96} \cdot {3}^{4}\text{.} \]
这意味着原值 \( x \) 必须小于81。唯一小于81的选项是80,因此答案是 \( A \) 。
~Nivek
解法2
\[ \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}} = \frac{{2}^{96}\left( \frac{{3}^{100}}{{2}^{96}}\right) + {2}^{96}\left( {2}^{4}\right) }{{2}^{96}{\left( \frac{3}{2}\right) }^{96} + {2}^{96}\left( 1\right) } = \frac{\frac{{3}^{100}}{{2}^{96}} + {2}^{4}}{{\left( \frac{3}{2}\right) }^{96} + 1} = \frac{\frac{{3}^{100}}{{2}^{100}} * {2}^{4} + {2}^{4}}{{\left( \frac{3}{2}\right) }^{96} + 1} = \frac{{2}^{4}\left( \frac{{3}^{100}}{{2}^{100}}\right) + 1}{{\left( \frac{3}{2}\right) }^{96} + 1}. \]
我们可以忽略末尾的1,因为它们几乎不会影响分数。因此,答案非常非常非常接近但略小于新的分数。
\[ \frac{{2}^{4}\left( {\frac{{3}^{100}}{{2}^{100}} + 1}\right) }{{\left( \frac{3}{2}\right) }^{96} + 1} < \frac{{2}^{4}\left( \frac{{3}^{100}}{{2}^{100}}\right) }{{\left( \frac{3}{2}\right) }^{96}} \]
\[ \frac{{2}^{4}\left( \frac{{3}^{100}}{{2}^{100}}\right) }{{\left( \frac{3}{2}\right) }^{96}} = \frac{{3}^{4}}{{2}^{4}} * {2}^{4} = {3}^{4} = {81} \]
所以,我们的最终答案非常接近但不到81,因此小于该数的最大整数是 \( A \) 80
解法3
设 \( x = {3}^{96} \) 且 \( y = {2}^{96} \) ,则我们的分数可写成 \( \frac{{81x} + {16y}}{x + y} = \frac{{16x} + {16y}}{x + y} + \frac{65x}{x + y} = {16} + \frac{65x}{x + y} \) 。注意到 \( \frac{65x}{x + y} < \frac{65x}{x} = {65} \) ,因此 \( {16} + \frac{65x}{x + y} < {16} + {65} = {81} \) 。而我们唯一小于81的选项是
解法4
设 \( x = \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}} \) 。两边同乘 \( \left( {{3}^{96} + {2}^{96}}\right) \) 并展开,整理项后得到 \( {3}^{96}\left( {{3}^{4} - x}\right) + {2}^{96}\left( {{2}^{4} - x}\right) = 0 \) 。左侧严格递减,且在 \( x = {81} \) 时为负。这意味着答案必小于81;因此答案为(A)
解法5(目测法)
更快的解法。意识到对于如此规模的指数, \( {3}^{n} \) 将远大于 \( {2}^{n} \) ,因此含2的项对商的影响极小。于是我们知道答案会非常接近81。
注意到分子和分母所加的项彼此成 \( \frac{1}{16} \) 的比例,因此它们必然会把比值从81稍微拉低。(就像一次低于你当前总评的新测验成绩总会把总评拉低一样。)答案:(A)。
解法6(利用选项)
我们可以把给定值与每个选项比较。已知它大于80,否则会有更小的答案,于是我们转向81。我们得到:
\[ \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}}?{3}^{4} \]
交叉相乘得:
\[ {3}^{100} + {2}^{100}?{3}^{100} + \left( {2}^{96}\right) \left( {3}^{4}\right) \]
约去 \( {3}^{100} \) 并除以 \( {2}^{96} \) 得 \( {2}^{4} \) ? \( {3}^{4} \) 。我们知道 \( {2}^{4} < {3}^{4} \) ,这意味着表达式小于81,故答案为(A)。
解法7(巧妙解法)
注意到 \( \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}} \) 可改写为
\( \frac{{81}({3}^{96}) + {16}({2}^{96})}{{3}^{96} + {2}^{96}} = \frac{{81}({3}^{96}) + {81}({2}^{96})}{{3}^{96} + {2}^{96}} - \frac{{65}({2}^{96})}{{3}^{96} + {2}^{96}} = {81} - \frac{{65}({2}^{96})}{{3}^{96} + {2}^{96}} \) 。注意
\( \frac{{65}\left( {2}^{96}\right) }{{3}^{96} + {2}^{96}} < 1 \) ,因此小于或等于 \( \frac{{3}^{100} + {2}^{100}}{{3}^{96} + {2}^{96}} \) 的最大整数是80,即(A)中的 \( \sigma D \) \( \sim \) blitzkrieg21
解法8
对于正数 \( a, b, c, d \) ,若 \( \frac{a}{b} < \frac{c}{\overline{d}} \) 则 \( \frac{c + a}{d + b} < \frac{c}{\overline{d}} \) 。令 \( a = {2}^{100}, b = {2}^{96}, c = {3}^{100}, d = {3}^{96} \) 。于是 \( \frac{c}{d} = {3}^{4} \) 。因此答案小于81,仅剩唯一选项80。
- 注意,此处的代数与解法5中的说明同义。这是代数层面的原因:若某次测验得分低于你的平均分(无论该测验占总成绩的分数或百分比是多少),都会拉低你的整体成绩。
~ ccx09
解法9
尝试长除法,可发现以 \( {3}^{4} = {81} \) 为分母过大,而以 \( {3}^{4} - 1 = {80} \) 为分母又过小。于是答案介于80与81之间,得80。
2018 AMC 10A 试题/第15题
两个半径为5的圆彼此外切,并同时内切于一个半径为13的圆,切点分别为 \( A \) 和 \( B \) ,如图所示。距离 \( {AB} \) 可表示为 \( \frac{n!}{n!} \) ,其中 \( m \) 和 \( n \) 为互质的正整数。求 \( m + n \) ?解法1
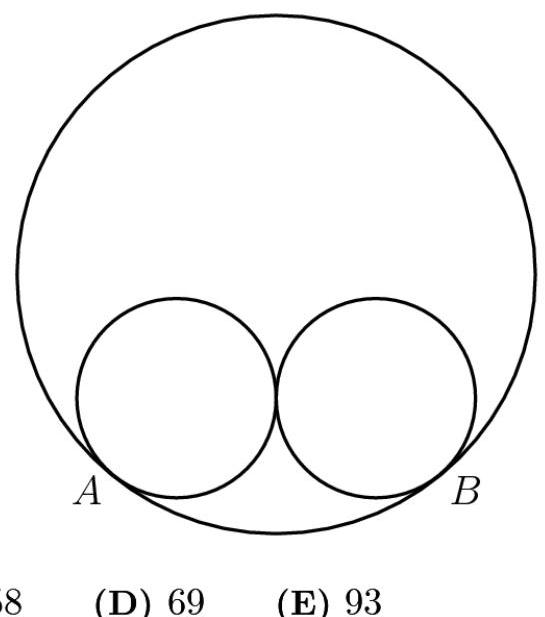
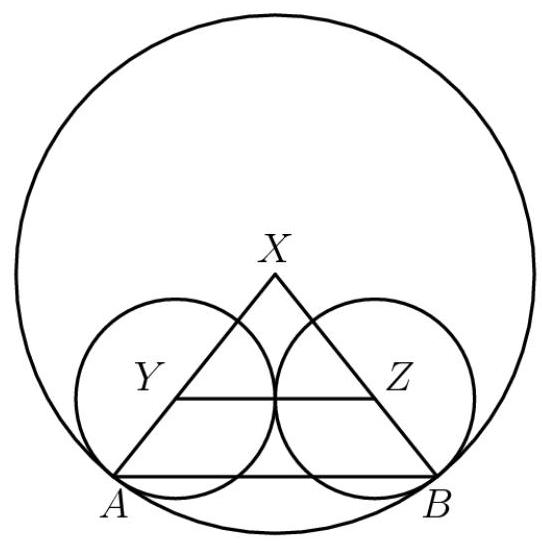
设大圆圆心为 \( X \) 。在点 \( A \) 处相切的圆以 \( Y \) 为圆心。同理,在点 \( B \) 处相切的圆以 \( Z \) 为圆心。连接 \( {AB} \) 、 \( {YZ} \) 、 \( {XA} \) 和 \( {XB} \) 。现可观察到 \( \bigtriangleup {XYZ} \) 与 \( \bigtriangleup {XAB} \) 相似。列出比例,得
\[ \frac{XY}{XA} = \frac{YZ}{AB} \Rightarrow \frac{{13} - 5}{13} = \frac{5 + 5}{AB} \Rightarrow \frac{8}{13} = \frac{10}{AB} \Rightarrow {AB} = \frac{65}{4}. \]
因此,答案为 \( {65} + 4 = D \) ) 69
解法2
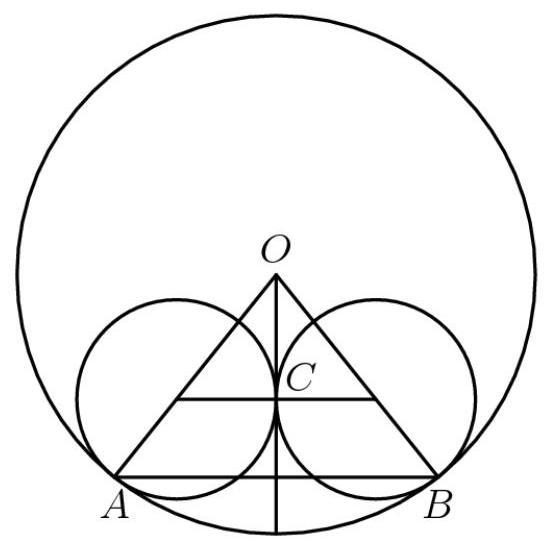
设大圆圆心为 \( O \) 。设两小圆的公切线为 \( C \) 。作大圆的两条半径 \( \overline{OA} \) 和 \( \overline{OB} \) ,以及两小圆到点 \( \underline{C} \) 的半径。作射线 \( \overrightarrow{OC} \) 和 \( \overline{AB} \) 。由此得到相似三角形,可解。由勾股定理, \( \overline{OC} \) 的长度等于 \( \sqrt{39} \) ,斜边长为8,另一直角边为5。利用相似三角形, \( {OB} \) 为13,因此 \( {AB} \) 的一半为 \( \frac{65}{8} \) 。
加倍得 \( \frac{65}{4} \) ,结果为 \( {65} + 4 = \) D) \( {69},{QED} \sqsubset \)
(elements2015 小幅编辑)
2018 AMC 10A 试题/第16题
直角三角形 \( {ABC} \) 的两条直角边长分别为 \( {AB} = {20} \) 和 \( {BC} = {21} \) 。包括 \( \overline{AB} \) 和 \( \overline{BC} \) 在内,从顶点 \( B \) 到斜边 \( {AC} \) 上的点可画出多少条整数长度的线段?(A)5 (B)8 (C)12 (D)13 (E)15
解法
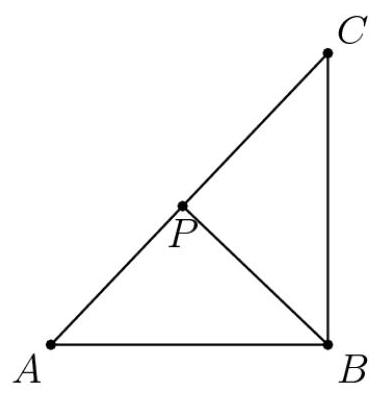
由于题目没有给出图形,我们自行绘制。斜边长度为29。设 \( P \) 为从 \( B \) 到 \( {AC} \) 所作垂线的垂足。注意 \( {BP} \) 是任何线段的最短可能长度。用两种方式写出三角形面积,即可解出 \( {BP} = \frac{{20} \cdot {21}}{29} \) ,其值介于14与15之间。
设线段为 \( {BX} \) ,其中 \( X \) 位于 \( {AC} \) 上。当 \( X \) 沿斜边从 \( A \) 移动到 \( P \) 时, \( {BX} \) 的长度严格递减,依次取遍20,19,…15这些整数值(介值定理)。同理,将 \( X \) 从 \( P \) 移动到 \( C \) 时,会依次取遍 \( {15},{16},\ldots ,{21} \) 的所有整数值。这样共有 \( \left| {\left( D\right) {13}}\right| \) 条线段。(asymptote图由elements2015添加)
2018 AMC 10A 试题/第17题
题目
设 \( S \) 是从 \( \{ 1,2,\ldots ,{12}\} \) 中选取的6个整数组成的集合,满足:若 \( a \) 和 \( b \) 是 \( S \) 的元素且 \( a < b \) ,则 \( b \) 不是 \( a \) 的倍数。 \( S \) 中元素的最小可能值是多少?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 7
解答
若从1开始,则无法再包含任何其他数,因此不可行。
若从2开始,就必须包含除1外的所有奇数来凑齐集合,但3和9会违反规则,因此也不可行。
尝试3同样行不通。可以加入7、11以及5或10(它们总是安全)。但再加入4或8后就无路可走。
最后,从4开始,我们发现序列4,5,6,7,9,11满足条件,故答案为(C) 4。(Random_Guy)
解答2
我们知道所有奇数(1除外)都可以使用。
\[ 3,5,7,9,{11} \]
现在剩下7个候选数可选(来自1,2,4,6,8,10,12)。可以排除1,2,10,12,剩下4,6,8可选。但9是3的倍数!于是必须从列表中去掉3或9。若去掉9,则所有数都不满足;若去掉3,则得到:
\[ 4,5,6,7,9,{11} \]
因此最小数为4,答案为 \( \mathbf{\left( C\right) }4 \) 。
2018 AMC 10A 试题/第18题
问题
有多少个非负整数可以写成如下形式
\[ {a}_{7} \cdot {3}^{7} + {a}_{6} \cdot {3}^{6} + {a}_{5} \cdot {3}^{5} + {a}_{4} \cdot {3}^{4} + {a}_{3} \cdot {3}^{3} + {a}_{2} \cdot {3}^{2} + {a}_{1} \cdot {3}^{1} + {a}_{0} \cdot {3}^{0}, \]
\( {a}_{i} \in \{ - 1,0,1\} \) 在哪里用于 \( 0 \leq i \leq 7 \) ?
(A) 512 (B) 729 (C) 1094 (D) 3281 (E) 59,048
解决方案 1
这看起来像是平衡三进制(balanced ternary),其中所有绝对值小于 \( \frac{{3}^{n}}{2} \) 的整数都用 \( n \) 位表示。共有8位。将8代入平衡三进制的公式,得到最大界限为 \( \left| x\right| = {3280.5} \) ,这意味着有3280个正整数、0和3280个负整数。由于我们只需要所有非负整数,因此共有 \( {3280} + 1 = {3281} \) 个整数,即 \( D \) 。
解决方案 2
注意,由该和式生成的所有数要么为正,要么为负,要么为零。由于对称性,由此和式生成的正数个数等于负数个数。只有一种方式能得到和为零,即所有 \( {a}_{i} = 0 \) 。从 \( i = 1,2,3,...7 \) 中选取 \( {a}_{i} \) 的总方式数为 \( {3}^{8} = {6561}.\frac{{6561} - 1}{2} = {3280} \) ,它给出了可能的负整数个数。题目要求非负整数的个数,因此从总数中减去该值得到 \( {6561} - {3280} = {3281} \) 。(RegularHexagon)
解决方案 3
注意,总可能性数(忽略题目所设条件)为 \( {3}^{8} = {6561} \) 。因此,E显然不现实。
请注意,如果 \( {a}_{7} \) 为1,则不可能
\[ {a}_{7} \cdot {3}^{7} + {a}_{6} \cdot {3}^{6} + {a}_{5} \cdot {3}^{5} + {a}_{4} \cdot {3}^{4} + {a}_{3} \cdot {3}^{3} + {a}_{2} \cdot {3}^{2} + {a}_{1} \cdot {3}^{1} + {a}_{0} \cdot {3}^{0}, \]
为负。因此,如果 \( {a}_{7} \) 为1,则有 \( {3}^{7} = {2187} \) 种可能。(我们还必须确信,这2187组不同的系数必然会产生2187个不同的整数结果。)
由于A、B、C均小于2187,答案必为 \( \left( D\right) {3281} \)
解决方案 4
注意,我们可以做一些简单的分类讨论:如果 \( {a}_{7} = 1 \) ,那么其余7个变量可以任意取值,因此这给我们 \( {3}^{7} \) 种情况。如果 \( {a}_{7} = 0 \) 且 \( {a}_{6} = 1 \) ,那么其余6个变量可以任意取值,给我们 \( {3}^{6} \) 种情况。如果 \( {a}_{7} = 0 \) 、 \( {a}_{6} = 0 \) 和 \( {a}_{5} = 1 \) ,那么我们得到 \( {3}^{5} \) 种情况。依此类推,我们共有 \( {3}^{7} + {3}^{6} + \cdots + {3}^{1} + {3}^{0} \) 种选择变量值的方式,但还需加1,因为我们尚未计入所有变量均为0的情况。因此,我们的总和为 \( \left| {\left( D\right) {3281}}\right| \) 。注意,我们已经统计了所有可能性,因为为了使该数非负,最大的正3的幂次必须大于或等于最大的负3的幂次。
解决方案5
关键在于意识到这个问题实际上发生在 \( a \in \{ 0,1,2\} \) ,如果每个 \( a \) 的值都增加1,本质上就变成了三进制(base 3)。那么范围将从 \( 0 \cdot {3}^{7} + 0 \cdot {3}^{6} + 0 \cdot {3}^{5} + 0 \cdot {3}^{4} + 0 \cdot {3}^{3} + \) \( 0 \cdot {3}^{2} + 0 \cdot {3}^{1} + 0 \cdot {3}^{0} = 0 \) 到 \( 2 \cdot {3}^{7} + 2 \cdot {3}^{6} + 2 \cdot {3}^{5} + 2 \cdot {3}^{4} + 2 \cdot {3}^{3} + 2 \cdot {3}^{2} + 2 \cdot {3}^{1} + 2 \cdot {3}^{0} = \) \( {3}^{8} - 1 = {6561} - 1 = {6560} \) ,产生6561个不同的值。由于题目最初给出的所有 \( {a}_{i} \in \{ - 1,0,1\} \) 的分布是对称的,我们保留3280个正整数和1个0,但舍弃3280个负整数。因此,我们得到答案,(D)3281。∎ --anna0kear
解决方案 6
首先,对所有 \( i \geq 1 \) 设置 \( {a}_{i} = 0 \) 。范围将是满足 \( \left\lbrack {-1,1}\right\rbrack \) 的整数。若对所有 \( i \geq 2 \) 都有 \( {a}_{i} = 0 \) ,则集合扩展为包含所有满足 \( - 4 \leq \mathbb{Z} \leq 4 \) 的整数。类似地,当 \( i \geq 3 \) 时得到 \( - {13} \leq \mathbb{Z} \leq {13} \) ,当 \( i \geq 4 \) 时范围为 \( - {40} \leq \mathbb{Z} \leq {40} \) 。该模式持续直至 \( i = 7 \) ,此时 \( - {3280} \leq \mathbb{Z} \leq {3280} \) 。由于我们只考虑正整数,需过滤掉所有 \( \mathbb{Z} < 0 \) ,最终得到介于 \( 0 \leq \mathbb{Z} \leq {3280} \) 之间的所有整数(含端点)。答案即为 \( \left| {\left( D\right) {3281}}\right| \) 。∎ --anna0kear
2018年AMC 10A试题/第19题
从集合 \( \{ {11},{13},{15},{17},{19}\} \) 中随机选取一个数 \( m \) ,再从 \( \{ {1999},{2000},{2001},\ldots ,{2018}\} \) 中随机选取一个数 \( n \) 。 \( {m}^{n} \) 的个位数字为1的概率是多少?
(A) \( \frac{1}{5} \) (B) \( \frac{1}{4} \) (C) \( \frac{3}{10} \) (D) \( \frac{7}{20} \) (E) \( \frac{2}{5} \)
解决方案 1
由于我们只关心个位数,我们的集合 \( \{ {11},{13},{15},{17},{19}\} \) 可以转化为 \( \{ 1,3,5,7,9\} \) 。称此集合为 \( A \) ,并称 \( \{ {1999},{2000},{2001},\cdots ,{2018}\} \) 集合为 \( B \) 。让我们根据从 \( A \) 中选取的元素进行分情况讨论。由于 \( 1 \cdot 1 = 1 \) , \( B \) 中的任何数都可以与1配对,使 \( {1}^{n} \) 的个位为1。因此,这种情况发生的概率为 \( \frac{1}{5} \) ,因为从 \( A \) 中选中1的概率为 \( \frac{1}{5} \) 。现在考虑从 \( A \) 中选中3的情况。让我们观察3不断自乘时的个位数:
\[ 3 \cdot 3 = 9 \]
\[ 9 \cdot 3 = 7 \]
\[ 7 \cdot 3 = 1 \]
\[ 1 \cdot 3 = 3 \]
我们发现,对于某个整数 \( x \) , \( {3}^{x} \) 的个位为1当且仅当 \( x \) 是4的倍数。现在,我们来统计 \( B \) 中有多少个数能被4整除。这可以通过简单列举完成:
2000,2004,2008,2012,2016.
在 \( B \) 中共有5个数能被4整除,而总共有 \( {2018} - {1999} + 1 = {20} \) 个数。因此,从 \( A \) 中选中3且从 \( B \) 中选中一个能被4整除的数的概率为 \( \frac{1}{5} \cdot \frac{5}{20} = \frac{1}{20} \) 。类似地,我们可以研究7的循环个位数:
\[ 7 \cdot 7 = 9 \]
\[ 9 \cdot 7 = 3 \]
\[ 3 \cdot 7 = 1 \]
\[ 1 \cdot 7 = 7 \]
我们发现,对于某个整数 \( y \) , \( {7}^{y} \) 的个位为1当且仅当 \( y \) 是4的倍数。这与我们刚才讨论3的情况条件完全相同,因此这种情况的概率也是 \( \frac{1}{20} \) 。由于 \( 5 \cdot 5 = {25} \) 且25以5结尾,对于某个整数 \( w \) , \( {5}^{w} \) 的个位始终为5。因此,这种情况的概率为0。最后需要讨论的是从 \( A \) 中选中9的情况,其发生概率为 \( \frac{1}{5} \) 。我们像之前对3和7那样列出9的循环个位数:
\[ 9 \cdot 9 = 1 \]
\[ 1 \cdot 9 = 9 \]
我们发现,对于某个整数 \( z \) , \( {9}^{z} \) 的个位为1当且仅当 \( z \) 为偶数。在 \( B \) 的20个数中,恰好有一半是偶数。因此,这种情况的概率为 \( \frac{1}{5} \cdot \frac{1}{2} = \frac{1}{10} \) 。最后,我们将所有概率相加得到
\[ \frac{1}{5} + \frac{1}{20} + \frac{1}{20} + \frac{1}{10} = 5 \]
~Nivek
解法2
由于只需关注个位数,我们可以将第一个集合转化为 \( \{ 1,3,5,7,9\} \) 。注意,对于所有奇数数字 \( x \) , \( {x}^{4} \equiv 1{\;\operatorname{mod}\;{10}} \) 成立,但5除外。观察第二个集合,它是1999到2018之间的所有整数。该集合共有20个元素,这意味着模4后,该集合有5个值对应 \( \{ 0,1,2,3\} \) ,使它们的概率相等。接下来,检查等于 \( 1{\;\operatorname{mod}\;{10}} \) 的值。共有 \( 4 + 1 + 0 + 1 + 2 = 8 \) 个值等于1,记住 \( {5}^{4n} \equiv 1{\;\operatorname{mod}\;{10}} \) 仅当 \( n = 0 \) 成立,而这里并不成立。总共有20个值,化简 \( \frac{8}{20} \) 得到 \( \left| \frac{2}{5}\right| \) 或 \( E \) 。
2018 AMC 10A 试题/第20题
扫描码由 \( 7 \times 7 \) 的方格网格组成,其中部分方格为黑色,其余为白色。在这49个方格中,必须至少包含每种颜色一个方格。若将整个方格绕其中心逆时针旋转 \( {90}^{ \circ } \) 的整数倍后外观不变,且沿连接对角顶点的直线或连接对边中点的直线反射后外观也不变,则称该扫描码为 \( \mathit{{symmetric}} \) 。问共有多少种可能的对称扫描码?
(A) 510 (B) 1022 (C) 8190 (D) 8192 (E) 65,534
解决方案 1
画一个 \( 7 \times 7 \) 正方形。
| K | J | H | G | H | J | K |
| J | F | E | D | E | F | J |
| H | E | C | B | C | E | H |
| G | D | B | A | B | D | G |
| H | E | C | B | C | E | H |
| J | F | E | D | E | F | J |
| K | J | H | G | H | J | K |
从中心开始,对称地标记所有突出的单元格。
更具体地说,由于存在4条给定的对称轴(2条对角线、1条垂直、1条水平),它们将图形划分为8个等价区域,我们只需取其中八分之一进行专门研究。每个区域包含10个不同的子方格,无论部分还是全部。由于每个子方格可涂成白色或黑色,我们最初有 \( {2}^{10} = {1024} \) 种选择,但需减去全白和全黑的2种情况,最终得到 \( \left( B\right) ,{1022} \) 。∎
我们实际只能决定10个方格的颜色,每个方格有2种独立选择,共 \( {2}^{10} = {1024} \) 种编码。根据规则必须至少包含两种颜色,需减去2种无效编码,最终答案为(B) 1022 "Nosysnow
注意此题与1996年AIME第7题极为相似。
解法2
2018 AMC 10A 试题/第21题
题目
以下哪项描述了实数 \( {xy} \) -平面中曲线 \( {x}^{2} + {y}^{2} = {a}^{2} \) 与 \( y = {x}^{2} - a \) 恰有3个交点时 \( a \) 的取值集合?
(A) \( a = \frac{1}{4} \) (B) \( \frac{1}{4} < a < \frac{1}{2} \) (C) \( a > \frac{1}{4} \) (D) \( a = \frac{1}{2} \) (E) \( a > \frac{1}{2} \)
解法1
将 \( y = {x}^{2} - a \) 代入 \( {x}^{2} + {y}^{2} = {a}^{2} \) ,得到
\[ {x}^{2} + {\left( {x}^{2} - a\right) }^{2} = {a}^{2} \Rightarrow {x}^{2} + {x}^{4} - {2a}{x}^{2} = 0 \Rightarrow {x}^{2}\left( {{x}^{2} - \left( {{2a} - 1}\right) }\right) = 0 \]
此为四次方程,共有4个根(含重根)。可见 \( x = 0 \) 始终存在至少一个交点(0, -a)(实为二重根)。
其余两个交点的 \( x \) 坐标为 \( \pm \sqrt{{2a} - 1} \) 。必须满足 \( {2a} - 1 > 0, \) ,否则抛物线将完全位于圆上方(仅在(0, a)处相切),导致实平面仅有一个交点。因此可得 \( \left( \mathbf{E}\right) a > \frac{1}{2} \) 。(projecteulerlover)
解法2
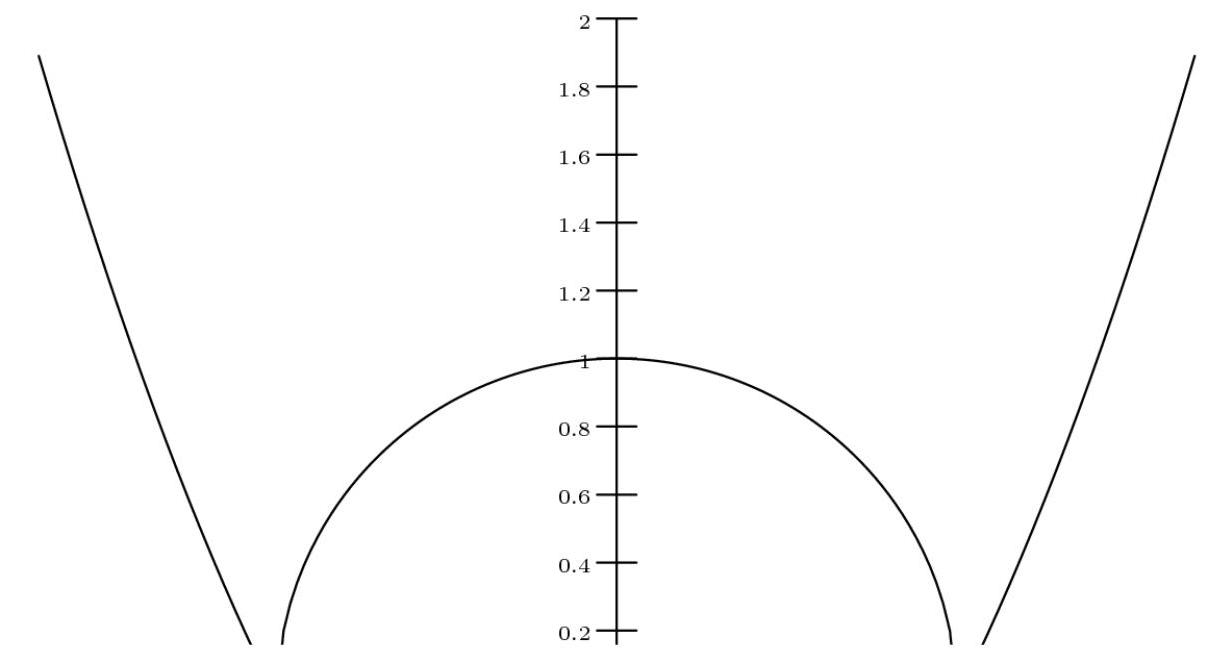
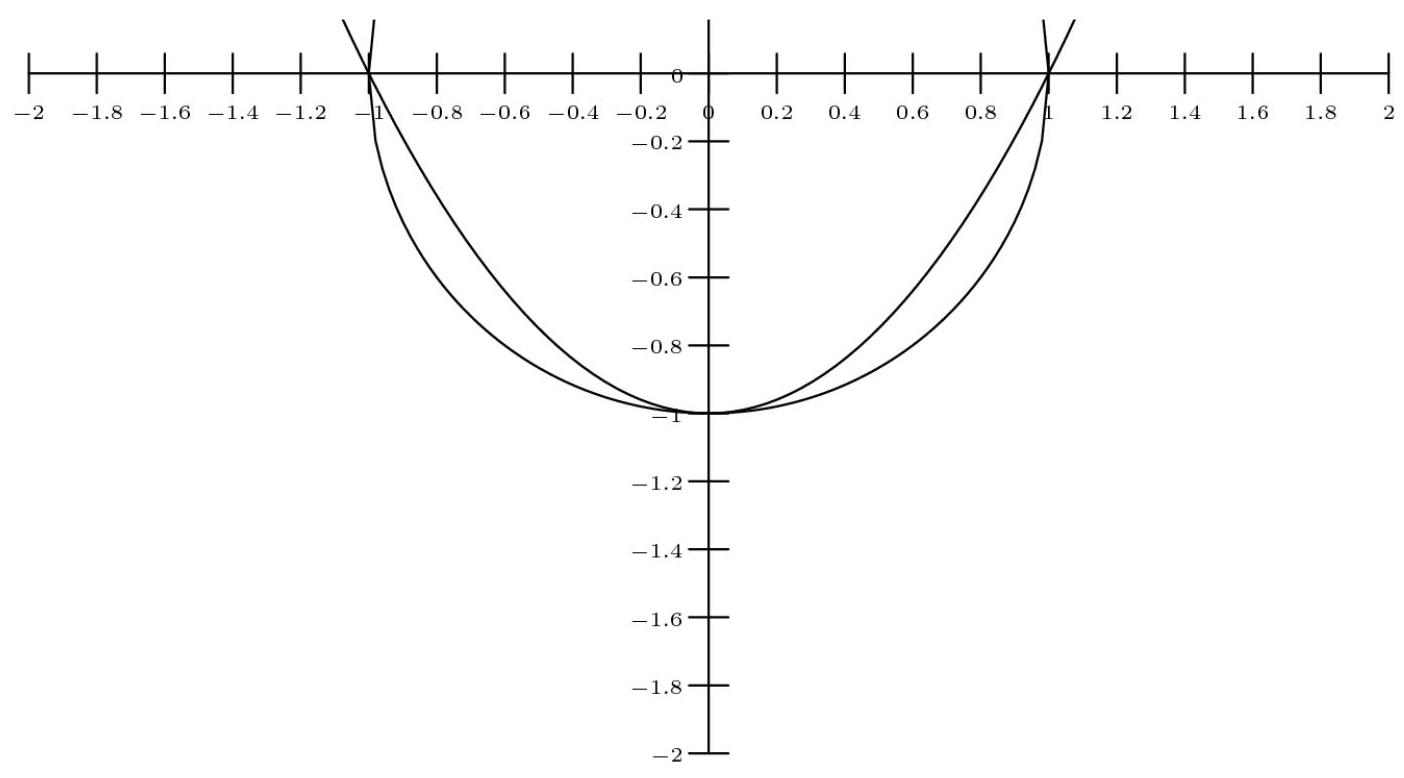
观察图像可知两曲线在(0, -a)相交。若抛物线"进入"圆内,则其"离开"时必然产生5个交点,这是不可能的。因此只需考虑抛物线与圆外切的情况。我们有 \( {x}^{2} - a = - \sqrt{{a}^{2} - {x}^{2}} \) 。两边平方并解得 \( {x}^{4} - \left( {{2a} - 1}\right) {x}^{2} = 0 \) 。由于 \( \mathrm{x} = 0 \) 已计入,仅需为 \( {x}^{2} = {2a} - 1 \) 求1个解,此时右侧函数显然单调递增。当a=1/2时x=0(重复计数),故 \( \left( \mathbf{E}\right) a > \frac{1}{2} \) 为正确答案。
解法提供者:JohnHankock
解法3
这描述了一个单位抛物线(unit parabola),其对称轴上有一个圆,且该圆与顶点相切。由于单位抛物线在顶点处的曲率(curvature)为2,与之匹配的圆的半径为 \( \frac{1}{2} \) 。该圆与一对无限接近的点相切,这两个点分别位于顶点两侧。因此,它仅与1个点相切。当使用更大的圆时,由于顶点两侧的点现在与顶点分离,它将与3个点相切。因此,(E) \( a > \frac{1}{2} \) 是正确的。
由于 \( \mathop{\lim }\limits_{{a \rightarrow \infty }}\left( {4{a}^{2} - {4a} + 1}\right) = \infty \) ,我们的范围是 \( \left( \mathbf{E}\right) a > \frac{1}{2} \) 。
解法由ktong提供
解法5(利用选项作弊)
只需代入 \( a = 0,\frac{1}{2},\frac{1}{4},1 \) 并解方程组。(这不会花太久。)然后发现只有 \( a = 1 \)
能为 \( x \) 产生三个实数解,因此我们完成,答案是 \( \mathbf{\left( E\right) }a > \frac{1}{2} \) 。
解法6(需用微积分)
为了求 \( a \) 的值,我们只需在将方程设为相等时计算根的重数(multiplicities):换句话说,取导数。我们知道 \( \sqrt{{x}^{2} - {a}^{2}} = {x}^{2} - a \) 。现在,两边平方并整理得到 \( {x}^{4} - \left( {{2a} + 1}\right) {x}^{2} + 2{a}^{2} = 0 \) 。接着,我们对方程取二阶导数得到 \( 6{x}^{2} - \left( {{4a} + 2}\right) = 0 \) 。现在,我们必须计算判别式(discriminant)。由于我们需要该方程的根为实数且不重复(否则它们不会在三个点相交),判别式必须大于零。因此,
\[ {b}^{2} - {4ac} > 0 \rightarrow 0 - 4\left( 6\right) \left( {{4a} + 2}\right) > 0 \rightarrow a > \frac{1}{2}\text{The answer is}\left( \mathbf{E}\right) a > \frac{1}{2}\text{and we are done.} \]
2018 AMC 10A 试题/第22题
设 \( a, b, c, \) 和 \( d \) 为正整数,使得 \( \gcd \left( {a, b}\right) = {24} \) 、 \( \gcd \left( {b, c}\right) = {36} \) 、 \( \gcd \left( {c, d}\right) = {54} \) 和 \( {70} < \gcd \left( {d, a}\right) < {100} \) 。以下哪个数必定是 \( a \) 的因数?
(A) 5 (B) 7 (C) 11 (D) 13 (E) 17
解法1
我们可以说 \( a \) 和 \( b \) “拥有” \( {2}^{3} * 3 \) , \( b \) 和 \( c \) 拥有 \( {2}^{2} * {3}^{2} \) , \( c \) 和 \( d \) 拥有 \( {3}^{3} * 2 \) 。将1和2结合可得 \( b \) 至少拥有 \( {2}^{3} * {3}^{2} \) ,因此 \( a \) 拥有 \( {2}^{3} * 3 \) (且不再拥有3的更高次幂,否则 \( {gcd}\left( {a, b}\right) \) 会不同)。此外, \( c \) 拥有 \( {3}^{3} * {2}^{2} \) ,因此 \( d \) 拥有 \( {3}^{3} * 2 \) (与 \( a \) 类似,我们看到 \( d \) 不能拥有2的更高次幂)。现在我们假设最简单情形,即 \( a = {2}^{3} * 3 \) 和 \( d = {3}^{3} * 2 \) 。根据此基例,我们得到 \( {gcd}\left( {a, d}\right) = 2 * 3 = 6 \) 。我们希望在两者之间再插入一个因子,使该数介于70与100之间,且这个新因子不能被2或3整除。逐一检验后,我们发现 \( 6 * {13} \) 是唯一可行的。因此答案为 \( \left( \mathbf{D}\right) {13} \)
JohnHankock的解法
解法1.1
进一步阐述解法1的观点:我们无法向 \( {gcd}\left( {a, d}\right) \) 再添加任何2或3的因子,因为那样会改变(a, b)与(c, d)的 \( {gcd} \) 。原因如下:
\( {gcd}\left( {a, b}\right) \) 是 \( {2}^{3} * 3 \) ,而(c, d)的 \( {gcd} \) 是 \( 2 * {3}^{3} \) 。然而, \( \left( {b, c}\right) = {2}^{2} * {3}^{2} \) 的 \( {gcd} \) (即两者都能被36整除)。因此, \( a \) 仅能被 \( {3}^{1} \) 整除(且不含3的更高次幂),而 \( d \) 仅能被 \( {2}^{1} \) 整除(且不含2的更高次幂)。
于是,(a, d)的 \( {gcd} \) 可表示为 \( 2 * 3 * k \) 的形式,其中 \( k \) 是一个不被2或3整除的数。唯一满足此条件(及其他条件)的选项是(D) 13。
解法2(更优记号)
首先注意24、36和54均形如 \( {2}^{x} \times {3}^{y} \) 。它们的质因数分解分别为 \( {2}^{3} \times {3}^{1} \) 、 \( {2}^{2} \times {3}^{2} \) 和 \( {2}^{1} \times {3}^{3} \) 。现设 \( {a}_{2} \) 和 \( {a}_{3} \) 分别为2和3在 \( a \) 中出现的次数。类似地定义 \( {b}_{2} \) 、 \( {b}_{3} \) 、 \( {c}_{2} \) 和 \( {c}_{3} \) 。现在将 \( {lcm} \) 转化为以下形式:
\[ \min \left( {{a}_{2},{b}_{2}}\right) = 3 \]
\[ \min \left( {{a}_{3},{b}_{3}}\right) = 1 \]
\[ \min \left( {{b}_{2},{c}_{2}}\right) = 2 \]
\[ \min \left( {{b}_{3},{c}_{3}}\right) = 2 \]
\[ \min \left( {{a}_{2},{c}_{2}}\right) = 1 \]
\[ \min \left( {{a}_{3},{c}_{3}}\right) = 3 \]
问题
农夫毕达哥拉斯有一块直角三角形的田地。该直角三角形的两条直角边长分别为3和4单位。在两条直角边相交成直角的那个角落,他留下一块未种植的小正方形 \( S \) ,从空中看就像直角符号。其余部分全部种植。从 \( S \) 到斜边的最短距离为2单位。问:田地中种植部分占几分之几?
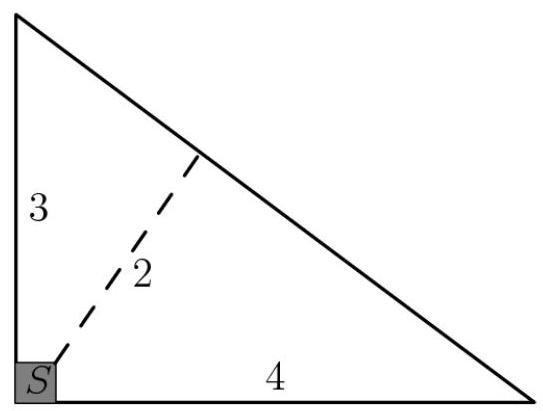
(A) \( \frac{25}{27} \) (B) \( \frac{26}{27} \) (C) \( \frac{73}{75} \) (D) \( \frac{145}{147} \) (E) \( \frac{74}{75} \)
解法1
设正方形的边长为 \( x \) 。将正方形 \( S \) 的右上角顶点与三角形斜边的两个顶点相连。这样就把三角形分割成若干区域,它们的面积之和必须等于整个三角形的面积,即6。
正方形 \( S \) 的面积为 \( {x}^{2} \) ,两个细长三角形区域的面积分别为 \( \frac{x\left( {3 - x}\right) }{2} \) 和 \( \frac{x\left( {4 - x}\right) }{2} \) 。最后,以斜边为底、高为2的三角形区域面积为5。于是我们有
\[ {x}^{2} + \frac{x\left( {3 - x}\right) }{2} + \frac{x\left( {4 - x}\right) }{2} + 5 = 6 \]
解得 \( x = \frac{2}{7} \) 。 \( S \) 的面积为 \( \frac{4}{49} \) ,所求比值为 \( \frac{6 - \frac{4}{49}}{6} = \frac{145}{147} \) 。
另一种方法:一旦得到 \( x = \frac{2}{7} \) ,可以不必计算,只需注意到分母中会出现7,因此答案的分母必须含因子7,只有 \( \left| \frac{145}{147}\right| \) 满足。
解法2
设正方形的边长为 \( s \) 。若将正方形的两边继续向三角形内部延长,直到与斜边相交于一点,我们将得到一个与斜边及两条新线构成的大相似直角三角形,以及两个共享长度为2的边的小相似三角形。利用这些三角形的边长比,可求得大相似三角形的长度为 \( \frac{5}{3}\left( 2\right) = \frac{10}{3} \) 。现在,将此大相似直角三角形向左延长,直到碰到长度为3的边。此时长度为 \( \frac{10}{3} + s \) ,利用边长比,其高为 \( \frac{3}{4}\left( {\frac{10}{3} + s}\right) = \frac{5}{2} + \frac{3s}{4} \) 。观察图形,若将此三角形的高与正方形边长相加,应得3,于是
\[ \frac{5}{2} + \frac{3s}{4} + s = \frac{5}{2} + \frac{7s}{4} = 3\frac{7s}{4} = \frac{1}{2}s = \frac{2}{7} \Rightarrow \text{area of square is}{\left( \frac{2}{7}\right) }^{2} = \frac{4}{49} \]
接下来是简单的部分:求面积比:
\[ \frac{3 \cdot 4 \cdot \frac{1}{2} - \frac{4}{49}}{3 \cdot 4 \cdot \frac{1}{2}} = \frac{6 - \frac{4}{49}}{6} = \frac{{294} - 4}{294} = \frac{290}{294} = \frac{145}{147} \]
ktong 提供解法
解法3
我们使用坐标几何。设直角位于(0,0),斜边为直线 \( {3x} + {4y} = {12} \) ,其中 \( 0 \leq x \leq 3 \) 。记 \( S \) 的位置为(s, s),根据点到直线的距离公式,可知
\[ \frac{\left| 3s + 4s - {12}\right| }{5} = 2 \]
\[ \Rightarrow \left| {{7s} - {12}}\right| = {10} \]
显然 \( s < \frac{22}{7} \) ,因此 \( s = \frac{2}{7} \) ,后续步骤可求得 \( \left| \frac{145}{147}\right| \) 。
解法4
设正方形边长为 \( x \) 。首先,用长度为2的线段与 \( S \) 的右上角构造一个相似三角形。因此,小三角形的最长边必为 \( 2 \cdot \frac{5}{4} = \frac{5}{2} \) 。接下来,用 \( x \) 表示该边并进行运算:从底边减去 \( x \) ,从顶边减去 \( \frac{3x}{4} \) 。于是得到方程
\( 3 - \frac{7x}{4} = \frac{5}{2} \) 。解得
\[ {12} - {7x} = {10} \Rightarrow x = \frac{2}{7}. \]
因此, \( {x}^{2} = \frac{4}{49} \) ,所以正方形覆盖三角形(面积为6)的比例为 \( \frac{2}{147} \) 。于是答案为 \( \left| \frac{145}{147}\right| \)
解决方案 5
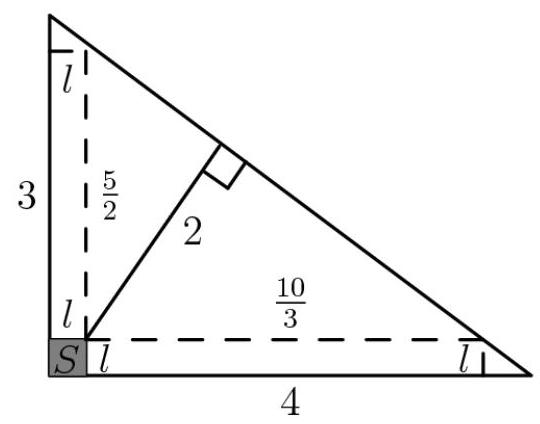
在上图中,找出两个与边长为3、4、5的大三角形相似的小三角形;因此,长度为 \( \frac{5}{2} \) 和 \( \frac{10}{3} \) 的线段。
求 \( l \) 的表达式:利用斜边,可得 \( \frac{3}{2} + \frac{8}{3} + \frac{5}{4}l + \frac{5}{3}l = 5 \) 。化简后得 \( \frac{35}{12}l = \frac{5}{6} \) ,即 \( l = 2/7 \) 。
另一种计算会得到 \( l + \frac{3}{4}l + \frac{5}{2} = 3 \) ,因此 \( \frac{7}{4}l = \frac{1}{2} \) 。换句话说, \( l = \frac{2}{7} \) ,同时为了验证,
\( l + \frac{4}{3}l + \frac{10}{3} = 4 \) 。因此, \( \frac{7}{3}l = \frac{2}{3} \) ,以及 \( l = \frac{2}{7} \) 。
最后,我们得到 \( A\left( {\square S}\right) = {l}^{2} = \frac{4}{49} \) ,从而完成解答。作为面积为6的三角形的一部分,答案应为 \( 1 - \frac{4}{{49} \cdot 6} = 1 - \frac{2}{147} = \frac{145}{147} \) ,因此 \( D \) 是正确的。∎ --anna0kear
解决方案 6
设 \( s \) 为正方形的边长。三角形的面积为6。将正方形内部的一个顶点与三个顶点相连,则三角形的面积也可表示为 \( 5 + \frac{3}{2}s + {2s} = 5 + \frac{7}{2}s \) 。解得 \( s = \frac{2}{7} \) 。因此答案为 \( \frac{6 - {\left( \frac{2}{7}\right) }^{2}}{6} = \frac{145}{147} \) 。D。
2018年AMC 10A试题/第24题
问题
三角形 \( {ABC} \) 与 \( {AB} = {50} \) 和 \( {AC} = {10} \) 的面积为 \( \underline{120} \) 。设 \( \underline{D} \) 为 \( \overline{AB} \) 的中点, \( E \) 为 \( \overline{AC} \) 的中点。 \( \angle {BAC} \) 的角平分线分别交 \( \overline{DE} \) 和 \( \overline{BC} \) 于 \( F \) 和 \( G \) 。求四边形 \( {FDBG} \) 的面积?
(A) 60 (B) 65 (C) 70 (D) 75 (E) 80
解决方案 1
设 \( {BC} = a \) 、 \( {BG} = x \) 、 \( {GC} = y \) ,且过 \( A \) 作 \( {BC} \) 的垂线长度为 \( h \) 。根据角平分线定理(angle bisector theorem),我们有
\[ \frac{50}{x} = \frac{10}{y} \]
其中 \( y = - x + a \) 。因此代入后我们得到 \( {BG} = \frac{5a}{6} \) 。根据相似三角形,我们有 \( {DF} = \frac{5a}{12} \) ,且该梯形的高为 \( \frac{h}{2} \) 。于是,我们得到 \( \frac{ah}{2} = {120} \) 。我们希望计算 \( \frac{5a}{8} \cdot \frac{h}{2} \) ,通过代入可知其值为75。
(rachanamadhu)
我可能读错了这个解法,但在我看来,作者错误地把角平分线当成了垂直平分线,这是不对的,因为该三角形并非等腰三角形。——bobert1
解法2
\( \overline{DE} \) 位于 \( A \) 到 \( \overline{BC} \) 的中点,且 \( {DE} = \frac{BC}{2} \) 。因此, \( \bigtriangleup {ADE} \) 是 \( \bigtriangleup {ABC} \) 面积的1/4,即30。接着,可算出四边形 \( {BD}\underline{EC} \) 的面积为 \( {120} - {30} = {90} \) 。与上一题类似,使用角平分线定理,可得 \( \overline{BG} \) 的长度是 \( \overline{GC} \) 的5倍。题目要求的是较大的那块。由于高相同,一个面积是另一个的5倍,于是 \( \frac{5}{6} \cdot {90} = {75} \) 。
解法3
由正弦定理, \( \bigtriangleup {ABG} \) 的面积与 \( \bigtriangleup {ACG} \) 的面积之比为 \( 5 : 1 \) 。因此 \( \bigtriangleup {ABG} \) 的面积为100。由于 \( \overline{DE} \) 是 \( \bigtriangleup {ABC} \) 的中位线,所以 \( {DF} \) 也是 \( \bigtriangleup {ABG} \) 的中位线。于是 \( \bigtriangleup {ACG} \) 与 \( \bigtriangleup {ABG} \) 的面积之比为1:4,故 \( \bigtriangleup {ACG} \) 的面积为25,由相似三角形可得。因此四边形 \( {FDBG} \) 的面积为 \( {100} - {25} = {75} \) (steakfails)
解法4
四边形 \( {FDBG} \) 的面积等于 \( \bigtriangleup {ABG} \) 的面积减去 \( \bigtriangleup {ADF} \) 的面积。注意到 \( \overline{DE}\left| \right| \overline{BC} \) ,于是 \( \bigtriangleup {ABG} \sim \bigtriangleup {ADF} \) ,又因为 \( \overline{AD} : \overline{AB} = 1 : 2 \) ,所以 \( \bigtriangleup {ADF} : \bigtriangleup {ABG} = {\left( 1 : 2\right) }^{2} = 1 : 4 \) 的面积为。
已知 \( \bigtriangleup {ABC} \) 的面积为120,在边 \( {AB} \) 上使用 \( \frac{bh}{2} \) 可得 \( \frac{50h}{2} = {120} \Rightarrow h = \frac{240}{50} = \frac{24}{5} \) 。由角平分线定理, \( \overline{BG} : \overline{BC} = {50} : \left( {{10} + {50}}\right) = 5 : \overline{6} \) ,因此
\( \bigtriangleup {ABG} : \bigtriangleup {ACB} = 5 : 6 \) 的高为。故答案为
\( \left\lbrack {FDBG}\right\rbrack = \left\lbrack {ABG}\right\rbrack - \left\lbrack {ADF}\right\rbrack = \left\lbrack {ABG}\right\rbrack \left( {1 - \frac{1}{4}}\right) = \frac{3}{4} \cdot \frac{bh}{2} = \frac{3}{8} \cdot {50} \cdot \frac{5}{6} \cdot \frac{24}{5} = \frac{3}{8} \cdot {200} = {75} \)
2018 AMC 10A 第25题
题目
对于正整数 \( n \) 及非零数字 \( a \) 、 \( b \) 和 \( c \) ,令 \( {A}_{n} \) 为所有位都是 \( a \) 的 \( n \) 位整数;令 \( {B}_{n} \) 为所有位都是 \( b \) 的 \( n \) 位整数;令 \( {C}_{n} \) 为所有位都是 \( c \) 的 \( {2n} \) 位(而非 \( n \) 位)整数。求 \( a + b + c \) 的最大可能值,使得存在至少两个不同的 \( n \) 满足 \( {C}_{n} - {B}_{n} = {A}_{n}^{2} \) ?
(A) 12 (B) 14 (C) 16 (D) 18 (E) 20
解法1
观察 \( {A}_{n} = a\left( {1 + {10} + \cdots + {10}^{n - 1}}\right) = a \cdot \frac{{10}^{n} - 1}{9} \) ;同理 \( {B}_{n} = b \cdot \frac{{10}^{n} - 1}{9} \) 和 \( {C}_{n} = c \cdot \frac{{10}^{2n} - 1}{9} \) 。关系式 \( {C}_{n} - {B}_{n} = {A}_{n}^{2} \) 可改写为
\[ c \cdot \frac{{10}^{2n} - 1}{9} - b \cdot \frac{{10}^{n} - 1}{9} = {a}^{2} \cdot {\left( \frac{{10}^{n} - 1}{9}\right) }^{2}. \]
由于 \( n > 0 \) 、 \( {10}^{n} > 1 \) ,我们可以约去 \( \frac{{10}^{n} - 1}{9} \) 的因子,得到
\[ c \cdot \left( {{10}^{n} + 1}\right) - b = {a}^{2} \cdot \frac{{10}^{n} - 1}{9}. \]
这是关于 \( {10}^{n} \) 的线性方程。因此,若有两个不同的 \( n \) 值满足它,则所有 \( n \) 值都满足。比较系数,我们需要
\[ c = \frac{{a}^{2}}{9}\text{ and }c - b = - \frac{{a}^{2}}{9} \Rightarrow b = \frac{2{a}^{2}}{9}. \]
为使 \( a + b + c = a + \frac{{a}^{2}}{3} \) 最大,需使 \( a \) 最大。由于 \( b \) 和 \( c \) 必须为整数, \( a \) 必须是3的倍数。若 \( a = 9 \) ,则 \( b \) 超过9。然而,若 \( a = 6 \) ,则 \( b = 8 \) 和 \( c = 4 \) ,答案为0.18(CantonMathGuy)
解法2(更快?)
立即尝试 \( n = 1 \) 和 \( n = 2 \) 。它们给出方程组 \( {11c} - b = {a}^{2} \) 和 \( {1111c} - {11b} = {\left( {11}a\right) }^{2} \) (化简为 \( {101c} - b = {11}{a}^{2} \) )。这意味着 \( {a}^{2} = {9c} \) ,因此可能的(a, c)对为(9,9)、(6,4)和(3,1)。第一种使 \( b \) 超出范围,但第二种使 \( b = 8 \) 。我们现在知道答案至少为 \( 6 + 8 + 4 = {18} \) 。
现在只需判断 \( a + b + c = {20} \) 是否可能对更大的 \( n \) 成立。我们总会得到形如 \( {100001c} - b = {11111}{a}^{2} \) 的方程,其中 \( c \) 的系数非常接近 \( a \) 系数的九倍。由于 \( b \) 项相当微小,我们再次知道 \( {a}^{2} \) 必须等于 \( {9c} \) ,因此 \( a = 9, c = 9 \) 是我们唯一可能达到20的希望。代入并除以9,我们将得到类似 \( {100001} - b/9 = {99999} \) 的式子。无论 \( n \) 实际为何, \( b \) 都超出范围(且显然不是2,而这是我们所需的)。
因此答案是 \( \left( D\right) {18} \)
解法3
注意到 \( {\left( 0.\overline{3}\right) }^{2} = 0.\overline{1} \) 和 \( {\left( 0.\overline{6}\right) }^{2} = 0.\overline{4} \) 。设 \( a = 3 \) 和 \( c = 1 \) ,我们发现 \( b = 2 \) 对所有可能的 \( n \) 值都成立。类似地,若 \( a = 6 \) 和 \( c = 4 \) ,则 \( b = 8 \) 对所有可能的 \( n \) 值都成立。第二种解给出更大的和(D) 18。